アンケート調査等のデータを扱う場面では、統計の基本的な指標である、基本統計量や分散・標準偏差に関する理解が欠かせません。これらの概念を正しく理解することで、データの傾向を正確に読み解き、調査結果の活用に関する精度を高めることができます。本記事は、これらの概念の定義や活用方法について例を用いてわかりやすく解説します。
データを解析する際に、データ全体の特性を把握するために使用される指標です。
主な基本統計量には以下があります。
- 代表値(そのデータ全体を表す値):最小値、最大値、中央値、最頻値、平均値
- 散布度(データの散らばりを表す値):範囲、分散、標準偏差、歪度、尖度
代表値とは
データの集まりを特徴づけるために、データ全体の傾向を示す数値のことです。
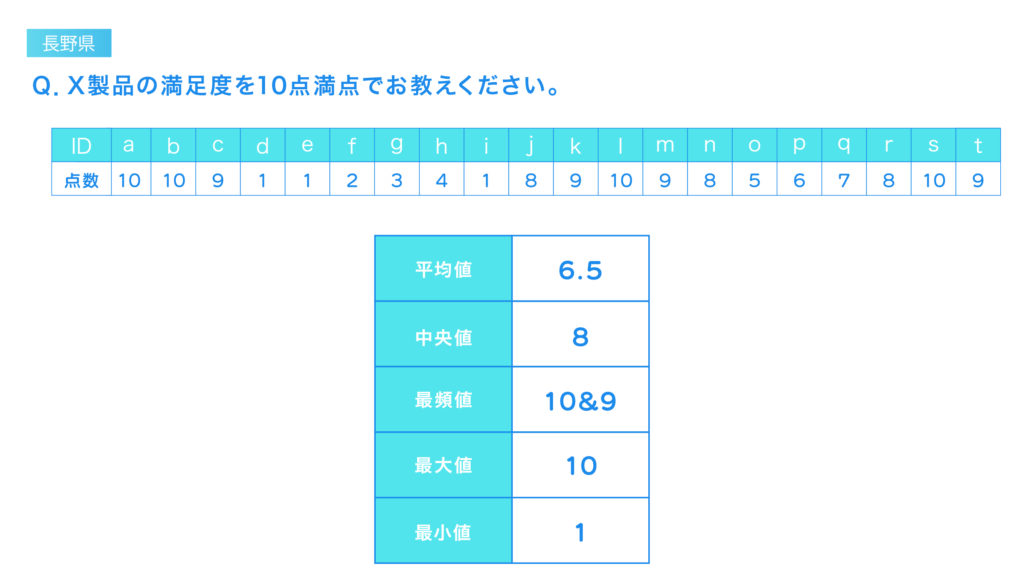
- 平均値(mean)
データの値を全て合計し、その件数で割った値です。全体の傾向を把握するための代表的な指標です。 - 中央値(median)
データを昇順に並べた際の真ん中に位置する値です。極端な値(外れ値)の影響を受けにくく、データの中心的な傾向を示します。
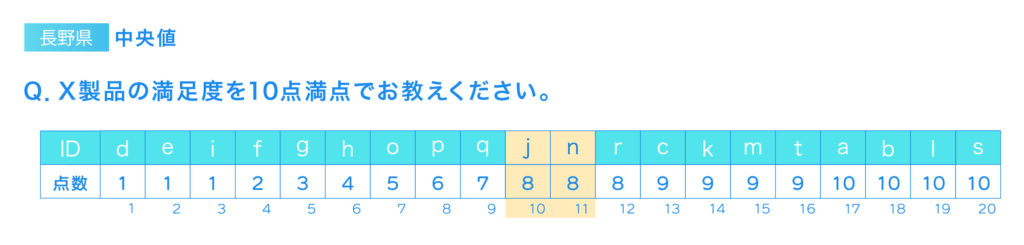
- 最頻値(mode)
データの中で最も頻繁に出現する値です。多くのデータが同じ値を持つ場合、その値が最頻値となります。例えば、消費者の選好がどの製品に集中しているかを知る際に役立ちます。 - 最大値(maximum)
データセット内の最も大きい値です。最高のパフォーマンスや最も高い数値を示す際に使用されます。 - 最小値(minimum)
データセット内の最も小さい値です。最低のパフォーマンスや最も低い数値を示す際に使用されます。
基本統計量は、データ全体を要約する際に便利ですが、特に次項で説明するように平均値は外れ値の影響を受けやすいため、最大値と最小値を確認することが重要です。外れ値があると、平均が不正確に上振れまたは下振れする可能性があります。平均値だけでは全体の分布を正確に把握できない場合があるため、分散や標準偏差を活用し、データのばらつきや広がりを測定することで、より正確なデータ解釈が可能となります。
以下のデータを参照してみましょう。
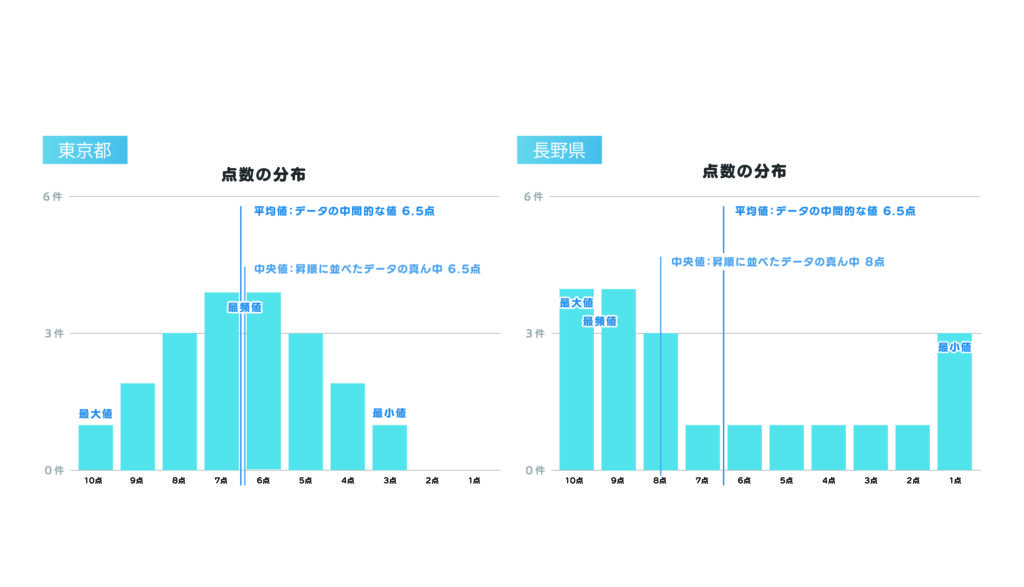
平均値は、データの中心的な傾向を示す指標ですが、下記のように東京都と長野県の平均点が同じであっても、両都県の傾向が同じとは限りません。
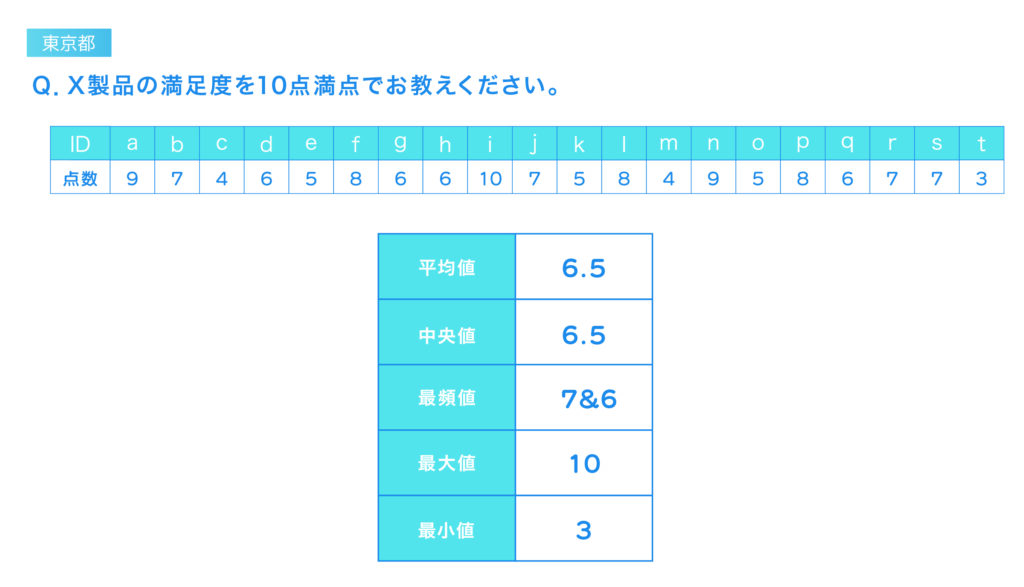
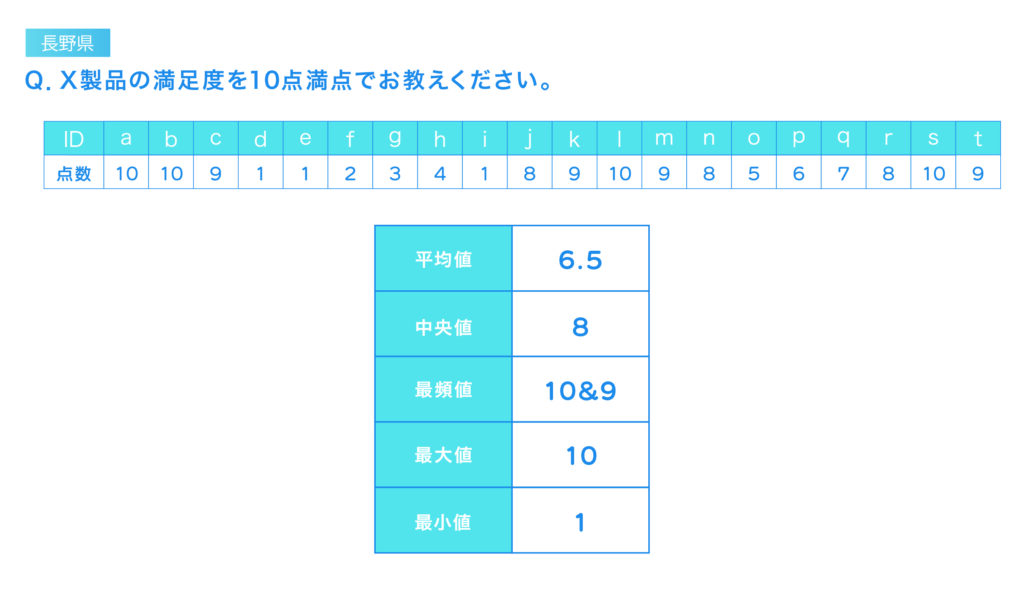
平均値は「外れ値(極端に高いまたは低い値)」の影響を受けやすいという弱点があります。
そのため下記のように、平均値が同じであってもデータの分布やばらつきが異なる場合、平均値のみを見て単純に同じように解釈し誤解を招く可能性があるのです。
散布度とは
散布度は、データ全体が平均からどれくらい散らばっているかを示すために重要な指標です。これらの統計量は、単に平均値を見るだけでは把握できないデータの散らばり具合を示し、データ全体の特徴をより正確に捉えるために用いられます。
- 分散(variance)
データの値と平均の差を二乗した合計を件数で割った値 - 標準偏差(standard deviation)
分散の平方根をとった値

先ほどのデータをもう一度参照してみましょう。
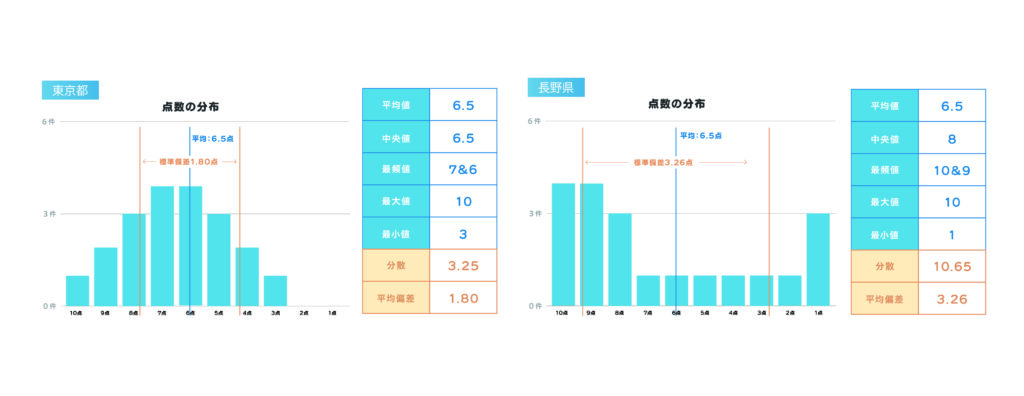
分散と標準偏差を見ると、平均値は同じでも、東京に比べて長野は分布が散らばっているということがわかります。
このように、分散や標準偏差は、図が無くとも数値のみでデータの傾向をより正確に捉えるための重要な指標です。
たとえば、標準偏差が大きい場合、データは平均から大きく散らばっていることを意味し、ばらつきが大きいと言えます。一方で、標準偏差が小さい場合、データは平均の周りに集中していることを示します。分散と標準偏差は、単に平均値を求めるだけでは見えないデータの特徴を捉えるために不可欠な指標なのです。
まとめ
本記事では、統計学の基本概念である基本統計量、分散、標準偏差について解説しました。
基本統計量は、データ全体の傾向を把握するための重要な指標であり、平均値、中央値、最頻値、最大値、最小値といった数値を用いることで、データの特徴を総合的に理解できます。
しかし、平均値は「外れ値(極端に高いまたは低い値)」の影響を受けやすいため、誤解を招く可能性があります。そのため、分散や標準偏差といった指標を活用し、データのばらつきや広がりを考慮することで、より精度の高いデータ解釈を目指していきましょう。
SKYFLAGリサーチについて

広告マネタイズプラットフォームの「SKYFLAG」を導入しているマンガアプリやゲームアプリなどさまざまなサービスで構成される独自のモニタからアンケート回答を取得できるマーケティングリサーチサービスです。
従来のアンケート回収の基盤となっているポイントサイト以外のユーザーからアンケート聴取ができるため、より市場の声に近い調査を行うことができます。
\ポイ活ユーザー以外に聞けるアンケート調査/




